King Roo has a set of four six-sided dice. If they're placed next to each other, they form all manner of four-digit numbers, as seen below.
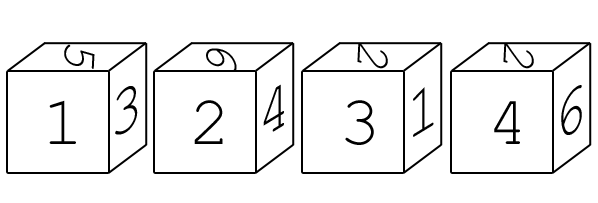
One day, after a long Dice-A-Roo session in the afternoon, he decided to take a break and find all the possible four-digit combinations these dice could form, including those with the six turned upsidown because, well, he's King so he can do what he wants.
After a bit of work, he found all the combinations, and then decided to take one more step...
If King Roo added up all the possible combinations formed by these four dice, what would the sum be?
Please enter just the number with no punctuation or formatting. (For example, 1,999 should be entered as 1999.)



very difficult :(
ReplyDeleteDo you include the 9 when 6 is turned upside down?
ReplyDeletek, thanks
Deleteanswer?
ReplyDeleteso basically you can get 1, 2, 3, 4, 5, 6, or 9 on one die
ReplyDeleteNot difficult, just going to take forever...
ReplyDeletecorrect all 7 numbers
ReplyDeleteThat's going to be an insanely big number!
ReplyDeleteIts 15,7698
ReplyDeletethx C:
DeleteHopefully you didn't submit that :) Don't be a sheep and believe everything you read.
DeleteMy brother says your math is wrong
DeleteThat is COMPLETELY off. The answer is 144, you DO NOT include 9.
Delete^ Yeah, I'm pretty sure that 157698 is WAY to big...
ReplyDeleteNot possible, there's 2401 combinations and even if all those combinations were the max possible number (9,9,9,9) the max is 86,463 so it can't be a number over that
ReplyDeleteNo, I just selected a handful of numbers and it came out to above that with just a few. Also, 9999 x 2401 is 24,007,599. Don't know where you got 86,463. But 157,698 is certainly within the realm of possibility. This is going to be a huge number, folks.
DeleteDafuq? You just multiplied 9999 by 2401... it's supposed to be(9+9+9+9) x 2401
DeleteU sure ???
ReplyDeleteYes.
ReplyDeleteEach combo is in the thousands and there is definitely more then 86 combos which means added up there is a sum much higher then 86,463.
ReplyDeleteDarn, I submitted the number of combinations before I read that it wanted the sum of all of the combinations. Oh well, I would probably skip this week's anyway because it would take forever to find the answer.
ReplyDelete1+1+1+1 = over 1000???
ReplyDeleteno, the 4-digit number would be 1,111.... Reread the the question
Deletehttp://www.puzzles.com/puzzleplayground/DiceSum/DiceSumSol.htm
ReplyDeleteThis looks like a similar problem but I can't be sure...
I think that's the answer :o
DeleteIt is. After looking at the link you gave and what is said in the LC, there is no doubt in my mind that is the same question and the same answer (On the link you provided.).
DeleteI used this answer but then realised that the difference is that Lenny wants ALL combinations and this page doesn't use repeated numbers (e.g. 2222 has not been included)
DeleteThere are 7 numbers (including 6 upsidedown being 9) and 4 dice. 7*7*7*7 = 2401. that's 2,401 different combinations of 1-6 + the number 9. Pretending that every combination is 9+9+9+9 (36) * 2401 = 86,436 so no. It's not bigger than that number
ReplyDelete4-digit number... READ PEOPLE!
DeleteIt isn't asking us to add the digits. 9999 is 9999.
DeleteOh ^.^
DeleteThat's the number of combinations, not the sum
DeleteI think we have two different interpretations going on here. Is it 1111+1112, or (1+1+1+1)+(1+1+1+2)?
ReplyDeletei think 1111+1112
DeleteThe correct answer is 3999600
ReplyDeleteYay! :)
DeleteCan you explain abit more on this?
DeleteCongrats you got it right Well done!!
DeleteI got the answer as 31,899,990. This was my theory:
ReplyDeleteSo we know the total combinations are 7*7*7*7 =2401. And so in the ones column (well this applies for all columns actually) there will is 2401 different possibilities yeah? And theoretically each number will be repeated the same amount of times. So 2401/7= 343. So therefore each number is in each spot 343 times.
Therefore the total of each column will be 343*1, 343*2, 343*3 etc = 10,290.
So you carry 1029 over to the tens column which then adds up to (10290+1029)=11319, so you place the 9 and carry the 1131 etc. Which finally gets you 31899990.
Does that make sense do you think?
Bro, can you explain abit more on this:
Delete"So you carry 1029 over to the tens column which then adds up to (10290+1029)=11319, so you place the 9 and carry the 1131 etc. Which finally gets you 31899990."
Why didnt you simply 10290*10 for the tens column, *100 for hundreds and *1000 for thousands then add the whole thingamagit together?
Correct method (but inefficient) but wrong answer :)
Delete"So you carry 1029 over to the tens column which then adds up to (10290+1029)=11319, so you place the 9 and carry the 1131 etc."
DeleteYes, but see, the next number would be the sum of the numbers plus what came from the previous column: 10290+ 1131 = 11421.
So, you showed that the last digits would be 90, with this, we place the 1 and it becomes 190, not the number you got in the end.
Its 3999600
ReplyDeleteWrong.
DeleteI shall explain why 3999600 IS NOT THE ANSWER :)
ReplyDeleteTHAT'S ONLY IF YOU AVOID DUPLICATES!
How can their be duplicates if your changing the numbers every combination?
DeleteBy duplicates I mean like, you can't get 1111 and stuff because there's multiple of same digit
DeleteYou guys are all idiots, by the way. All of these answers are wrong. Good luck, morons, finding your own answer.
ReplyDeleteMaybe this is will be the question where those who can actually figure it out will keep their goddamn mouths shut and bring home a cool million.
Well it ain't going to be you. ^.^
DeleteToo late for that :/
DeleteI just entered all the possible combos into excell, and used autosum to get the final answer - 11431079
ReplyDeleteFinally, someone gets it right!
DeleteStill wrong but you're very close... Last 4 digits are wrong.
DeleteNo, This one is right - Maybe check your own last four digits?
Deletehttp://www.puzzles.com/puzzleplayground/DiceSum/DiceSumSol.htm
DeleteAll you have to do is replace 3 numbers in that problem and you get the answer. The procedure is exactly the same except for one very simple difference..
I did that and got 11432190. That should be right, but it's always best to not believe me because it could still be wrong.
Delete^ is correct.
DeleteYou must have messed up. I'm pretty sure the first guy got it right.
DeleteThe last number has to be a 0:
DeleteEqual numbers of "1"s and "9"s, equal numbers of "6" and "4", equal numbers of "2", "3" and "5".
Hence the first post "11431079" is off.
Hello
ReplyDeletesoo do we add all the combinations up from 1111 to 9999 or do we just find all the different possible combinations?
how to find the answer...open Microsoft Excel, in the first box type 1111 then the next one down 1112 then the next 1113 then highlight them, click and drag the small box in the corner all the way down till it says 9999. once you have done that press CTRL+F and find one at a time the numbers you don't want (7,8,0) click 'find all' an for each one do CTRL+A in in the find box then click on Excel and DEL until all the numbers containing 7,8 and 0 are deleted (double check all theses numbers are gone by using the find method again) once this is done click the box below the 9999 and use the auto sum tool (make sure you select all the way back up to 1111) and this should give you the answer. I'm not actually going to tell you the answer I got but I hope this helped :3
ReplyDeleteI believe this is the correct method and I got 11432190
DeleteHint: all answers posted so far are incorrect
ReplyDeleteFind it yourself if you don't want to facepalm yourself when the answer you submitted is very close to the real answer but not exactly.
"If they're placed next to each other, they form all manner of four-digit numbers, as seen below."
ReplyDeleteThat means the first die uses 1,3,5, the second die uses 2,4,6 (and 9), the third die uses 1,2,3, and the fourth die uses 2,4,6 (and 9). Therefore 3 possibilities for the 1st die and 3rd die each, 4 possibilities for the 2nd and 4th die each. Multiply, 144 combinations. Write em down and add em up :)
Sorry but that is incorrect.
Deleteso what is the answer if that is incorrect?
DeleteWait if he says add all the combination up maybe just add the amount of combination up?
ReplyDeleteyeah i think so.
Deletedidnt he say to add up all the combination?
ReplyDeleteI know how to do this but my excel isnt working so to do this on word or my notepad is gonna take me forever. I hope after all this I get it right.
ReplyDeleteWell I tried it on Excel. (Took me like 30 minutes)
ReplyDeleteAnd by using a series of complicated functions, I got an answer in the hundred millions.
So either I am way off or you are all way off.
By the way, you there are not just a series of 1-6 in 4 rows, but 5 rows since the 6 can be upside down.
So rows 1-4 are counted 1,1,1,1,6 then 1,1,1,2,6
There are only 4 die so how can there be 5 rows?
DeleteWait when they say with the 6 upside down, does that mean it's not a 6 but a 9?
ReplyDeleteMeans theres a 6 and a 9 that can be counted...
DeleteI still believe its 4 rows u just have to use 9 as well so 1111 1112 1113 1114 1115 1116 1119 is the first set of 1s then 1121 1122 1123 thats how I been doing it but since excel isnt working for me Its taking me forever to do it myself and totaling the scores.
ReplyDeleteI did that with excel. Done in 10 minutes but it's a pain...
Deleteis it 23,997,600? i counted using permutation
ReplyDeletesorry 3,999,600
DeleteI find it sad that people are struggling with this when the answer/how to get the answer is up there.
ReplyDeletePeople just don't know how to read
Deleteproblem is there are so many... how do you know which is correct.. and many just talk as if they know it all but don't provide a working solution...
DeleteThe answer is 11432190.
ReplyDeleteWhat I did:
int nums[7] = {1, 2, 3, 4, 5, 6, 9};
int sum = 0;
for (int i = 0; i < 7; i++)
{
int thousands = nums[i] * 1000;
for (int j = 0; j < 7; j++)
{
int hundreds = nums[j] * 100;
for (int k = 0; k < 7; k++)
{
int tens = nums[k] * 10;
for(int l = 0; l < 7; l++)
{
int ones = nums[l];
sum += thousands + hundreds + tens + ones;
}
}
}
}
//sum ends up with the value of 11432190
I believe that this is the right answer... although presented in a very computerish style.
DeleteOk i cant understand a thing of what he does but this is how i believe it should be solved (purely by words hence can be long winded but should be easier to understand) EDIT: there is a post above with a similar working too!:
You have 4 Dice, numbers (1,2,3,4,5,6,9) and you can form any number using the dice. What we need is the total sum of all the possible combinations of the dice.
Working out each and every number would yield (7*7*7*7) 2401 possible numbers (hence you would not want to calculate it individually as some people stated above seem to have tried)
Looking at the "ones" there are 2401 possible numbers and all numbers are used equally. Hence out of the 7 possible numbers, each number will be used 2401/7 = 343 times. Now taking 343 and multiplying by each number (1,2,3,4,5,6,9) and then totaling up the sum, you should get (343*30) = 10290
By the same logic, in the "tens" there are also 2401 possible numbers, but now they are as follows: (10,20,30,40,50,60,90). Taking each number and multiplying by 343 will yield 102900 (see the pattern?)
Filling in the "hundreds" and "thousands" column likewise, you will eventually end up with these numbers: 10290, 102900, 1029000, 10290000
Now, adding these numbers altogether at you get: 11432190
Arg, I got 11422190, but i did the amounts for 9111 through 9999. I did a long round about way of finding the totals then found the totals for each group of 9111 - 9911, 9121 - 9921, et cetera. Found the total for all the 111, etc not including the 9000 so that I would have a base for the other thousand numbers 1000 - 6000. Added the needed about of thousands for each number 1 - 6 since I already had 9 done then added the base... Its overly complicated but I hope I got it right, your ever so slightly different answer and easier solution makes me nervous :p
Deleteproblem is that im not sure if its only the number that it would land on I.E. a six landing any way is still a six even if it looks like a nine without knowing that there is no way to be sure
DeleteAnyone else got 8 digits with the sum of 27?
ReplyDeleteI got 10746190. I may have missed something, but the way I figured this out (using Excel) did make sense...
ReplyDeleteI got 10552390. I did it with excel!!!! I think is the right answer. I did it calculating individually (1111, 1112... 1999) Then I add all this numbers, This results plus 7000 (7870+7000, 7940+7000....) I did the same with the number three and so on. I Completed all, then I add it all and I got this number. It make sense!!!
ReplyDeleteYeah It's not that sum people don't read it's that we read EVERYTHING and don't know who's right and who to believe. So my only option is to do it myself manually but its taking me forever and I'm adding it myself with a calculator. since I'm doing 1111 1112 etc into 1211 1212 1213 1214 etc. then have to do all the 2s,3s,4s,5s,6s,and 9s it can be done but I''m worried after all this work I wont even earn a trophy. So I kinda hope a lot of people get it wrong no offense cuz I know if anyone does it this way u'll get the right answer it just takes 4ever.
ReplyDeletealthough,thats kinda confuing....i tried it then i kept pressing 7 & 8 and i kept forgetting to do double number....
DeleteI second 11432190.
ReplyDeletetot := 0; numList := [1, 2, 3, 4, 5, 6, 9]; counter := 1;
while counter <= 840 do
for i to 7 do
for j to 7 do
for k to 7 do
for l to 7 do
tot := tot+1000*numList[i]+100*numList[j]+10*numList[k]+numList[l];
counter := counter+1
end do;
end do;
end do;
end do;
end do;
tot ends up as 11432190
Yay programming! :)
Deleteok there are waaaay too many different answers. maybe were all wrong?
ReplyDeleteI miraculously got 2599590.......
ReplyDeleteits 14189920
ReplyDeleteI got 11359127. Here's a pdf of my findings: http://dl.dropbox.com/u/33417912/lenny%20conundrum.pdf
ReplyDeleteI just added all the numbers highlighted in blue for the number I got.
There would be only 6 numbers on the dice at any time whether one of them is a 6 or 9 and only 1 dice may have the 6 upside down to form a 9 ...I think anyway...Too hard for me I am afraid...
ReplyDeleteI changed the formula on http://www.puzzles.com/puzzleplayground/DiceSum/DiceSumSol.htm to work for combinations (replace the 6*5*4 by 7*7*7) and found: 1143219 (same as the guy earlier) i submitted this :)
ReplyDeleteI got 2401
ReplyDeleteI really should know this-I'm doing probability in school...
ReplyDeleteYou should take this problem into school them:)
ReplyDeleteAhem. *cough* *cough* The answer is 144. 4 dice, 6 sides, multiply those together, 24. Multiply 24 by 6 sides and you get 144. The answer is 144 for sure.
ReplyDeleteThey said 9 sides because the king likes to use the 6 upside down
Delete1111, 1112, 1113, 1114, 1115, 1116, 1119, 1121, 1122, 1123, 1124, 1125, 1126, 1129, 1131, 1132, 1133, 1134, 1135, 1136, 1139, 1141, 1142, 1143, 1144, 1145, 1146, 1149, 1151. 1152, 1153, 1154, 1155, 1156, 1159, 1161, 1162, 1163, 1164, 1165, 1166, 1169, 1191, 1192, 1193, 1194, 1195, 1196, 1199, 1211. 1212, 1213, 1214, 1215, 1216, 1219, 1221, 1223, 1224, 1225, 1226, 1229, 1311, 1312, 1314, 1315, 1316, 1319, 1331, 1332, 1333, 1334, 1335, 1336, 1339, 1411, 1412, 1413, 1414, 1415, 1416, 1419, 1441, 1442, 1443, 1444, 1445, 1446, 1449, 1511, 1512, 1513, 1514, 1515, 1516, 1519, 1551, 1552, 1553, 1554, 1555, 1556, 1559, 1611, 1612, 1613, 1614, 1615, 1616, 1619,
ReplyDelete1661, 1662, 1663, 1664, 1665, 1666, 1669,
So up there is all the combinations that star with one so you would have to do that 9 times. Instead take all 117x 9= 1053
^ sorry if that isn't right it just seems correct i guess
But that would include the 7 and 8 so you have to subtracted off of that making it 819
Deletei got 700+. i may have misinterpreted the question. not sure if the question requires you to add up the total number of combinations or to add up the digits in the combinations. i took the meaning of the question as the former lol
ReplyDeleteI laugh at everyone who got some really stupid answers when the answer was right in front of you: 3,999,600 was the CORRECT answer.
ReplyDeleteHere is the link to where the answer lies: http://www.puzzles.com/puzzleplayground/DiceSum/DiceSumSol.htm It was the same question, same rules and everything
that is the answer to the problem you post but if they dont give the same info it should not be the answer they have
Deletefunny how you are laughing when you just copied someone else's answer online that wasn't even to teh same problem... you got lucky, and you didnt get the correct answer
DeleteLC made a mistake by not including the rule that duplicates werent allowed. I hope they change the results so that everyone who just went online and copied got it wrong and the ones that actually worked for the answer got it right
The rules on that puzzle are not the same. There was nothing on the LC about avoiding duplicates. TNT messed up this one...
ReplyDeleteI agree- sometime TNT does mess up the LC and I think this is one of those times. The puzzle asked for all four digit combinations, not just those with no duplicates, so the answer, if you got your computer to come up with all the possible 2401 numbers and add them up should be 11432190. But oh well, TNT will do what they want regardless of the math....
ReplyDelete