Arty loves to garden! In fact, he has quite a large one in the back of his shop that he keeps all to himself. It's 55 yards wide and 40 yards long with a diagonal path, one yard wide, running through it. Erm... maybe this will help:
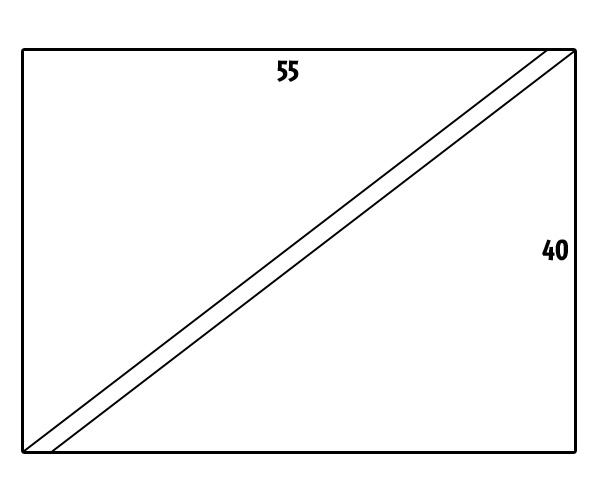
Okay, so, it's not to scale. Arty's a gardener, not an architect! Anyway, he'd like to cover the path with some nice pebbles, but he's unsure of how much he'll need to buy. First he needs to know how big the path is!
What is the area of the path?
Enter the number in square yards, rounding to the nearest whole number.



40?
ReplyDeleteDiagonal of a rectagle= square root of side squared + side squared. The squares and the square root sign cancel out so it' 44+ 50. So it
ReplyDelete's 94ft long?
Use Pythagorean's Theorem. (a^2)+(b^2) = c^3.
ReplyDelete(55^2)+(40^2) = c^2.
c^2 = 68.007
ROUND TO NEAREST WHOLE NUMBER AND LEAVE ANSWER IN SQUARE YARDS
So, the answer would be:
68 square yards
Pythag is for triangles.
ReplyDeleteOH LOL I GET IT THE TRIANGLE IN THE RECTANGLE.
ReplyDeletebut doesn't it matter how wide it is?
and there are 2 equal triangles which are 55 x 40 x 68
ReplyDeleteIf you submit the correct answer right now, what are the chances you won?
ReplyDeletebut it is a parallellogram as well?
ReplyDeleteI got 68 square yards as well. I know I didn't make it in time though(so even if my answer is wrong, I'm not too hung up over it).
ReplyDeleteisn't 68 yards implying the distance of the hypotenuse length but not the AREA...?
ReplyDeletearea of square minus area of 2 triangles
ReplyDelete55*40-54*40=40
It is NOT 68. The height of the triangle is indeed 40, but is the base 55? Check again. You'll see that the Pythagorean formula is not applicable here (though it IS necessary in some part of this calculation). If you've taken Geometry, you should have enough knowledge to solve this, though it's pretty hard (it's a conundrum after all).
ReplyDeletehow does one write square yard?
ReplyDeletesquare yard?
sq yd?
yd²?
yd2?
X 3X
I think 40 is right - the rectangle has an area of 2200, each triangle has an area of 1080. 2200-1080-1080=40.
ReplyDeleteThe left over area is the path.
Let's see: The whole area measure 55*40 and consider that the triangles are (1/2)54*40. Thus, the area covered by triangles is 54*40, so the area to be covered is 55*40-54*40 which is 40. Simple, really. Too bad I only got home right now
ReplyDeleteHaha. It is 40. You just solve for the area of a parallelogram (40 times 1 yard = 40).
ReplyDeleteLook at the pathway as a parallelogram. Find the diagonal section by using the Pythagorean theorem, but MAKE SURE that you do 55-1 because that 55 includes the 1 yard that is the width of the path. So the actual base of the triangle is 54, not 55. If you find the diagonal and use that to find the area of the parallelogram, you will find the area of the path.
ReplyDelete55-1=54
(54^2)+(40^2)=c^2
c^2=4516
c=67.201 (This is the diagonal length)
67.201*1(width of path)=67.201 square yards.
Round the decimal. Answer is 67.
I thought that to calculate the area of a parallelogram you had to multiply the base with the height, not the length of the side...
ReplyDelete132
ReplyDelete((55-1)+40)/2*V2
how big the path is
^ this is what he wants
it's 57.
ReplyDelete50 is the answer.
ReplyDeleteTake the Pythagorean Theorem to find the triangle within the side corner, approximate the two side rectangles within the edge of the path, and you get 50. Simple. Oh dear I might be wrong though.
It's 68. Use the phythagorean theorem to find the base of the parallelogram. It's 68.007. We already know the path is 1 yard wide, so that's be the height. b*h=a. 68.007*1+68.007. Round up. 68 square yards!
ReplyDeleteWow you guys are making this waaay too difficult. Use the pythag to find that 40^2 + 55^2 gives you 4625. Square root is the base of the parallelo, then times the height which is one as denoted by the statement. Calm yourselves lol!
ReplyDeleteHAHAHA
ReplyDeleteNone of you got it correct yet.
Keep trying, n00bs.
I'll let you guys know when one of you get it right.
ReplyDeleteIt's 68.
ReplyDelete68
ReplyDelete66.6666= 67
ReplyDelete(55)(40) - x = \sqrt{x^2 - 40^2} (40)=67
ReplyDeleteI got 67.
ReplyDeleteWhy are people using 55-1 as a side? 1 is the width of the path, once it reaches the 55 side, the path is at an angle to the side. that means the side of the triangle is less than 54, because the length of the path along the side is greater than 1.
ReplyDeleteWow. So many wrong answers. But there's one correct too. Most of you really suck at this, don't you?
ReplyDelete40 lol area of parallelogram is base x height
ReplyDelete1 x 40= 40
68 square yards
ReplyDeleteYou are making it so difficult!
ReplyDeleteThe area of the whole garden is 55 × 40 = 2200 yards. The area beside the path is a triangle so we calculate this area: 0,5((55-1)×40)) = 1080. Now, we have 2 triangles, so it is 1080 × 2 = 2160. Triangle + triangle + path = garden area, therefore 2160 + path = 2200, therefore gardenarea - 2triangles = path, so 2200 - 2160 = 40. I hope you guys get it now ;)! No parallelogram calculation needed lol.
I like how you act like the parallelogram calculation is hard. It's just base times height. 1 yard x 40 yards = 40 yards^2. As you can see, both answers are correct, but this way was much easier lol.
ReplyDeleteIt is hard. The base isn't 1 and the height isn't 40 either. The height is very very small and the base is like 67..
ReplyDeleteI hope you guys realize that the 55 including the path, which means you don't have to subtract anything. Thats just making the path shorter. And your answer too small. And to those of you using the 2 triangle/ parallelogram approach, the end of the path that is along the 55 yard side is longer than 1. You don't have enough information to figure out how long it actually is without using trig. The answer is 68.
ReplyDeleteAhhhh nevermind it's wrong, it's 67
ReplyDelete1/sinus(45) gets something like 1.4, 55-1.6=53.6 then 53.6²+40²=4471
ReplyDeletesquareroot= 66.86= 67, which is the base,
times height which is 1 = still 67.
the answer is 57 I think...
ReplyDeleteIt would make sense: the small side from the 55, is square root 2 = 1.414... (since you can see a smaller triangle there, with both sides being 1)
So then two ways to calculate: Area of parallellogram => base * height = 1.414... * 40 = 56.5 = 57
Whole area minus the two triangles =>
(55 *40) - ((55-1.414...)* 40) = 56.5 = 57
This is only true if the other side from the smaller traingle is also 1, which I am not entirely sure of. But since it's a parallel diagnol I think this is case.
Lol nevermind it's 67. Found a way to calculate it three times, abc-formula and all that jazz. Worked a lot better lol.
ReplyDeleteLol nevermind it isn't.
ReplyDeleteThe path isn't 1 yard wide at the end, it's √2 wide.
ReplyDeleteOnce you understand this picture, you will also understand that it is 57
ReplyDeletehttp://tinypic.com/r/2zrdc1e/7
The guy who said 66.66666 (so 67) is right. Like I said, the large triangles are 40 yards by a little less than 55 yards. Hint: Use similar triangles.
ReplyDelete2*(a+b)= 2*(55+40)=190
ReplyDeleteThe triangles are 40*53,6=2144 and the whole area 40*55=2200. I don't know how you get 67 out of it...
ReplyDeletehow did you get 53,6?
ReplyDeleteI typed in 68 and it told me it was correct. Simple Pythagorus. 55*55= 3 025 40*40=1600
ReplyDeleteadd them together you get 4625. You just then square root it and *1. I did wonder how so may people got it wrong, then I saw this board
XD Lenny Conundrum told you it was correct? 53,5858 comes from the fact that the path is 1 yard wide and 1,4142 wide at the end.
ReplyDeleteFINALLY!!
ReplyDeleteYep, the answer is 53,6585 = 54!
Finally I mean, I thought no one would get it right like me xD
ReplyDeleteLearn simple maths and then come online to complain! the answer is 57. You saw it proved above.
ReplyDeleteI know simple math and I am pretty sure it's 54.
ReplyDeleteI will be laughing my ass off, when they tell you it's 57. Or 56 if TNT screws up the rounding up again.
ReplyDelete40,67,68
ReplyDeletePythagoras is not needed for this exceedingly simple problem. You can either tae the entire rectangle and substract the two triangles or look at the path as the paralellogram it is. Both methods will yield you 40, the correct answer.
ReplyDeleteThere is no way it even could be 40. The path is clearly longer than the 40 yard long side. If the path was 40 square yards, it would have to be 40 yards long as it is stated that it's 1 yard wide.
ReplyDelete40 sounds plausible in hindsight, but it is not. Though 57 sounds odd, it has a better chance of winning than 40. Oh well, hoping my early submission of 67 does the trick.
ReplyDeleteYOU GUYS ARE IDIOTS!!!!! First of all, i think the 40 theory sounds most logical to me and also it says to enter your number in SQUARE YARDS therefore the answer should be 40 sq. yds.
ReplyDeleteYou guys are making this WAY MORE COMPLICATED than it actually is...
ReplyDeleteLet me answer this for you. The area of the entire rectangle is 2200. (55x40=2200)
ReplyDeleteTo figure out the area of the path, you must figure out the area of both triangles. Given that the path is one yard wide, the base and height of both triangles is 54 and 40... so you just need to multiply 54 by 40 and subtract that from 2200. (yes the area of a triangle is 1/2(b*h) but both triangles are the same size so its unnecessary to divide by half and add them together)
The answer is 40sq. yards. 2200-2160=40
Otherwise correct, but the base of the triangle IS NOT 54!
ReplyDeletehttp://tinypic.com/r/2zrdc1e/7
As you can see in this picture the red line is the mentioned one yard. The blue line is therefore the squareroot of two. Which makes the base of the triangle 53.5858 yards.
40*53.5858=2143.432
2200-2143.432=56.568=57
I still go with my answer of 57 (56.5)
ReplyDeleteI hope I win a bigger loot this round. I was the first one to reply to this thread with 57 as an answer. Lol.
Answer is 67 or (66.6666666)
ReplyDeleteFormulas Needed: Pythagoras and area of a parallelogram
Lets call the little section from the side 55 as "X" an unknown value
40^2 + (55-X)^2 = 40X^2 (40x because parallelogram is base x Height, we know the height of 40 but no base.) That = X^2 - 110X + 4625 = 1600X^2
Rearrange by taking them all on the left across = 1599X^2 +100X - 4625 = 0
Now the Quadratic Formula
-B ± (Square root)/b^2-(4AC)
---------------------------
(2 x A)
Therefore: =
______________________
-110x ± √110^2 - (4x1599x-4625)
--------------------------------- = 5/3 or 1.67
(2 x 1599)
x= 1.6666666 so (55-x) = (55 - 1.66666) = 53.333
Last but not least pythagoras as 1 yard would not affect the area from the hypotenuse of the triangle= 53.333^2 + 40^2 = 4444.44444 then square root 4444.4444 = 66.66666666 rounder up = 67!!!
Peace ^^
40^2 + (55-X)^2 = 40X^2
ReplyDelete^ I have no idea what you are calculating with this? 40x would be the area of the path, not the length of the hypotenuse.
Okay it's either 68 or 67 or 40. 68/67 I gathered from using pythagoras theorem and then multiply by the width (1) which left 68. However, I realised that the triangle is NOT actually 55 long... the path is 1 yard wide so it is actually 54.
ReplyDeleteSo, I got 67 that way.
Then I realised that the path is not a rectangle so you can't just use the worked out sides and times it by 1.. (can you?)
Sooo what I did is worked out the added areas of both triangles 2( 1/2 * 40 * 54 )and then that answer subtracted from the total area of the entire garden. So, what is left is the area of the path.
However, neopets say 'round to the nearest number' so yeah...
TNT says 64???
ReplyDeleteTNT is assuredly wrong. The answer is DEFINITELY 67 (200/3, or 66.66666...). Some of the answers above have complete explanations for it being 67.
ReplyDeleteHow do we tell them they're wrong?
Seriously... is this just a case of "life isn't fair?"
ReplyDeletewhat the huck
ReplyDeleteIt's a case of sometimes people screw the heck up.
ReplyDelete64?!?!?!? Are they insane?! How did they come up with that?!
ReplyDeleteOH! Maybe the path is 1 meter wide PERPENDICULAR to the path. We were all using the idea that the path is 1 meter wide parallel to the sides of the garden. If you do the math that way, then instead of the path being 1 meter "wide", you have to use a right triangle with arctan(40/55) and one leg being one meter wide, so you'd have to figure the area of the path using a width of 1/cos(arctan(40/55))=1.23649. Which means the path should have an area of...
ReplyDelete49.46?
Somebody want to double-check my math? I thought I had this cracked, but apparently not.
Its 67, my friend and I used autocad on this and that cannot be wrong.
ReplyDelete